RC-цепь: постоянная времени
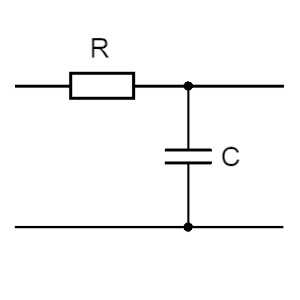
RC-цепь (резистор-конденсаторная цепь) — одна из самых простых электронных схем. Как нетрудно догадаться из названия, она состоит из резистора и конденсатора, соединённых последовательно или параллельно. Не смотря на простоту, эта цепь способна применять довольно сложные математические операции к входным сигналам, а также управлять продолжительностью во времени разных электронных событий.
Краткое содержание:
- Принцип работы RC-цепи
- Постоянная времени
- Расчёт RC-цепи
- Интегрирующая RC-цепь
- Дифференцирующая RC-цепь
- Примеры схем
Принцип работы RC-цепи
Если к RC-цепочке подключить источник питания, конденсатор начнёт заряжаться через резистор.
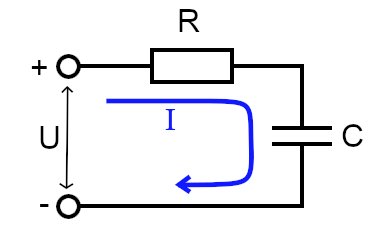
Заряд конденсатора
Этот процесс растянут во времени. Резистор ограничивает ток: чем выше его сопротивление, тем медленнее идёт заряд. С другой стороны, от ёмкости конденсатора зависит, какое количество заряда он способен принять: чем больше ёмкость, тем дольше он будет заряжаться. Процесс происходит до тех пор, пока конденсатор не зарядится полностью. Тогда на нём установится напряжение питания U, а ток в цепи прекратится.
Нужно отметить, что заряд конденсатора происходит по экспоненциальному закону, то есть скорость заряда (другими словами, ток в цепи) уменьшается со временем. Ведь чем больше заряда накопил конденсатор, тем сложнее впихнуть в него очередную порцию.
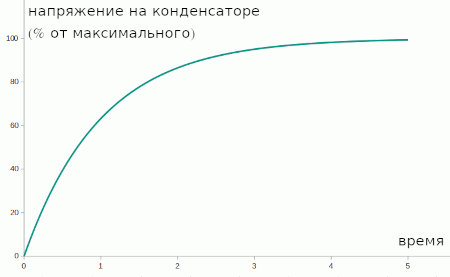
Зависимость напряжения на конденсаторе от времени
Аналогично происходит разряд конденсатора через резистор. Только напряжение на кондесаторе со временем не растёт, а падает, и скорость этого процесса по тем же законам постепенно замедляется.
Постоянная времени
Всё вышесказанное математически выражается через постоянную времени τ (тау). Это ключевой параметр RC-цепи, который показывает, за какое время конденсатор зарядится до 63% от максимального значения или разрядится до 37% от начального значения.
Постоянная времени рассчитывается по формуле:
τ = R × C
Где:
- R — сопротивление резистора в омах
- C — ёмкость конденсатора в фарадах
Чем больше значение постоянной времени, тем медленнее происходит заряд или разряд конденсатора.
Откуда взялись числа 63% и 37%? Почему, например, не 80 и 20? Здесь мы имеем дело со стандартным подходом к измерению экспоненциальных процессов, к слову, не только в электронике. Постоянная времени показывает, за какое время величина изменяется в e раз. Здесь e - основание натурального логарифма. Это одна из основных констант математики, примерно равная 2.71.
Допустим, конденсатор разряжается. Через время, равное τ, его заряд уменьшится в e раз и станет равным 1/e ≈ 0.37 или 37% от начального. Через следюущий промежуток τзаряд уменьшится ещё в e раз и т.д.
Аналогично, при заряде за каждый последующий период τ заряд увеличивается на (1 - 1/e), или 63% от разницы между текущим и максимальным зарядом. Математически это означает, что заряд конденсатора будет бесконечно приближаться к максимальному, но никогда его не достигнет. На практике, считается, что конденсатор полностью заряжен через время 5 * τ. На графике выше шкала времени как раз размечена в единицах τ.
Расчёт RC-цепи
С помощью приведённых формул можно точно рассчитать напряжение на конденсаторе в каждый момент времени. Допустим, такая задачка. Есть RC-цепочка из резистора 100 Ом и конденсатора 2000 мкФ. Её подключили к источнику питания с напряжением 10 В. Через какой промежуток времени напряжение на конденсаторе достигнет 8 В?
Сначала посчитаем постоянную времени:
τ = 100 * 0.002 = 0.2 с
Теперь посчитаем, за сколько периодов τ напряжение достигнет 80% от максимального:
n = -ln(1-0.8) ≈ 1.6
Чуть больше полутора периодов. Осталось посчитать это в секундах:
t = 0.2 * 1.6 = 0.32 c
Интегрирующая RC-цепь
Интегрирующая RC-цепь — это схема, в которой выходное напряжение пропорционально интегралу входного сигнала по времени.
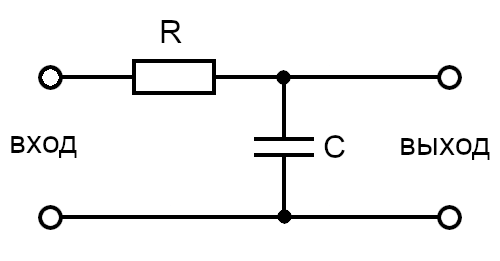
Интегрирующая RC-цепь
Давайте посмотрим, как она работает, на примере простых сигналов. Для начала, подадим на вход интегрирующей цепи прямоугольный импульс большой длительности.
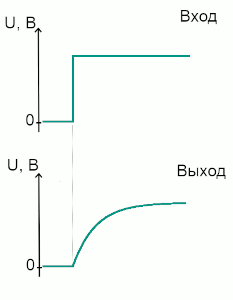
Прямоугольный импульс на входе интегрирующей RC-цепи
Постойте! Интеграл от константы - линейная функция, а у нас на выходе явно кривая. Собственно, это кривая заряда конденсатора, рассмотренная выше.
Дело в том, что, если взять выходной сигнал на очень маленьком интервале времени, наша кривая практически совпадает с линейной. И тогда противоречий нет. А мы делаем первый вывод: интегрирующая RC-цепь хорошо работает только с сигналами, у которых период значительно меньше постоянной времени τ.
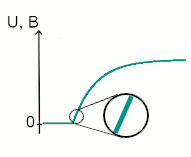
Линейный участок на кривой заряда конденсатора
Интегрирование ШИМ-сигнала
Что ж, давайте подадим на вход те же прямоугольные импульсы, но высокой частоты:
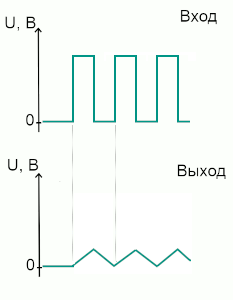
Более высокочастотный сигнал на входе даёт пилообразное напряжение на выходе
Здесь наша RC-цепочка работает в линейной области. Предполагается, что к выходу схемы подключена нагрузка, через которую конденсатор разряжается в промежутке между импульсами.
При дальнейшем увеличении частоты сигнал на выходе становится практически постоянным: за короткий импульс конденсатор не успевает заметно зарядиться, но и за паузу не разряжается полностью, как в предыдущем примере.
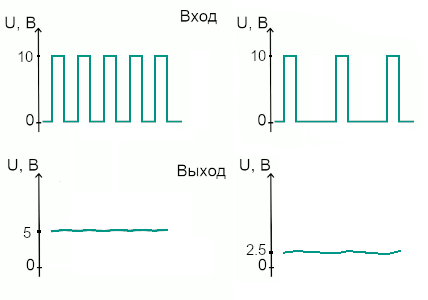
Ещё поднимаем частоту входного сигнала. Интегрируем ШИМ-сигнал
Обратите внимание: уровнь сигнала на выходе напрямую зависит от скважности импульсов. Таким образом, RC-цепочка прекрасно работает с ШИМ-сигналом, превращая его в постоянное напряжение заданного уровня.
RC-цепочка в цепи переменного тока
Выше мы видели, как интегрирующая RC-цепь "сглаживает" ШИМ-сигнал, приводя его к некоему постоянному усреднённому напряжению. То же самое будет происходить, если на вход подать гармонический (синусоидальный) сигнал достаточно высокой частоты.
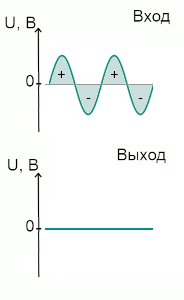
Гармонический сигнал на входе интегрирующей RC-цепи. Положительные и отрицательные участки имеют одинаковую площадь и взаимно компенсируются при интегрировании
Вспомним, что интеграл - это, по сути, суммарная площадь под кривой, с учётом знака. В данном случае площадь положительных участков, которые выше нуля, полностью сопадает с площадью отрицательных. Они взаимоуничтожаются и на выходе получается ноль.
Но что, если мы приподнимем сигнал, добавим к нему постоянную составляющую? Интегрирующая RC-цепь и в этом случае сгладит сигнал, убрав все "неровности". Другими словами, выделит постоянную составляющую.
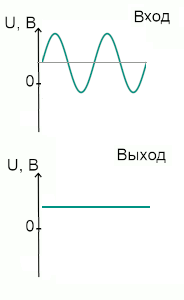
Выделение постоянной составляющей входного сигнала
Можно посмотреть на это ещё вот с какой стороны. Резистор и конденсатор представляют собой делитель напряжения. Выходной сигнал в этой схеме снимается с нижнего плеча делителя, с конденсатора. При этом, сопротивление конденсатора зависит от частоты сигнала: чем она выше, тем меньше сопротивление. Получается, такой делитель ослабляет высокочастотную составляющую входного сигнала, т.к. вся эта составляющая падает на верхнем плече делителя, резисторе.
Применение интегрирующей RC-цепи
Подводя итог характеристикам и применению интегрирующей RC-цепи:
- Постоянная времени должна быть много больше времени изменения входного сигнала
- В сочетании с источником ШИМ-сигнала позволяет получать постоянное напряжение заданного уровня
- Служит фильтром высоких частот
- Позволяет выделить постоянную составляющую
Дифференцирующая RC-цепь
Если в интегрирующей RC-цепи поменять резистор и кондесатор местами, получится дифференцирующая RC-цепь.
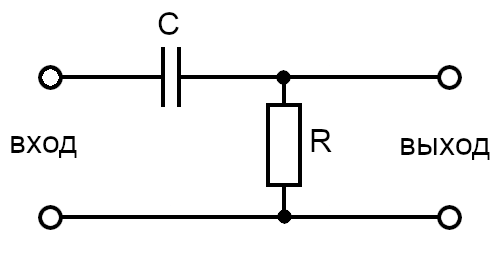
Дифференцирующая RC-цепь
Как не сложно догадаться из названия, в дифференцирующей RC-цепи выходное напряжение пропорционально производной входного сигнала по времени.
Почему так происходит? Здесь мы тоже имеем дело с делителем напряжения, только верхнее плёчо представлено конденсатором, а нижнее - резистором. Для постоянного сигнала сопротивление конденсатора высокое, он просто не пропускает постоянную составляющую к резистору (соответственно, к выходу). Зато для изменяющегося сигнала сопротивление конденсатора низкое. Чем круче изменяется входной сигнал - тем ниже сопротивление конденсатора - тем большая доля напряжения сигнала будет доставаться резистору. Это и есть взятие производной. Ведь производная в математике показывает скорость изменения функции.
Формирователь импульсов
Подадим на вход дифференцирующей RC-цепи длинный прямоугольный импульс. Как и ожидалось, в момент переднего фронта импульса скорость изменения входного сигнала максимальна, поэтому и на выходе всплеск напряжения. Но затем конденсатор начинает потихоньку заряжаться проходящим через него током, показывая нелинейную картину.
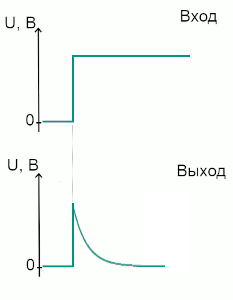
Прямоугольный импульс большой длительности на входе дифференцирующей RC-цепи
Поэтому, дифференцирующая цепь, так же, как интегрирующая, хорошо работает на высоких частотах, чтобы период сигнала был много меньше постоянной времени τ.
Но и на длинных имульсах дифференцирующая цепь находит своё применение. Если пренебречь пологим и нелинейным задним фронтом выходного сигнала, получается, мы сформировали короткий выходной импульс из длинного входного. Причём параметры выходного импульса (длительность) определяются постоянной времени. Таким образом, дифференцирующая RC-цепочка может использоваться в цифровой электронике как формирователь импульсов.
Прохождение высокочастотного сигнала
На высоких частотах RC-цепь показывает хорошее дифференцирование, при этом форма выходного сигнала повторяет форму входного. Но, без постоянной составляющей: производная константы, как известно, равна нулю.
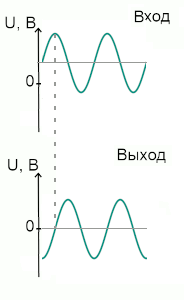
Дифференцирующая RC-цепь сохраняет форму сигнала, но убирает постоянную составляющую
Применение дифференцирующей RC-цепи
Кратко подведём итог сказанному о дифференцирующей RC-цепи. Она может применяться:
- В схемах формирования импульсов
- В качестве фильтра низких частот
- Позволяет убрать постоянную составляющую сигнала
Примеры схем
В практических схемах, размещённых на данном сайте, есть примеры применения RC-цепей. Могу порекомендовать вашему вниманию: модель реле времени с времязадающей RC-цепочкой и генератор прямоугольных импульсов. Также RC-цепь используется как фильтр постоянной составляющей при соединении каскадов усилителя, например, в этой схеме.




Добавить комментарий