Колебательный контур
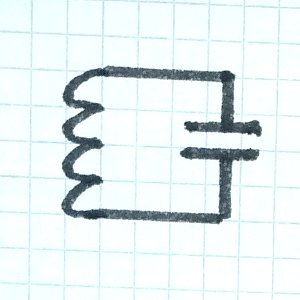
Колебательный контур — это цепь, состоящая из конденсатора и катушки индуктивности. Колебательный контур — частый элемент радиосхем, поэтому есть смысл познакомиться с протекающими там процессами более подробно.
Краткое содержание статьи:
- Процессы в колебательном контуре
- Расчёт частоты колебаний
- Добротность
- Аналогия с механической системой
- Применение колебательного контура в схемах
Процессы в колебательном контуре
Как следует из названия, дело будет связано с колебаниями. Точнее говоря, с электромагнитными колебаниями. Представим, что мы зарядили конденсатор до некоторого напряжения, и подключили к нему катушку индуктивности. Что будет происходить в этой цепи?
Конденсатор начнёт разряжаться через катушку индуктивности. Если вместо катушки взять металлическую перемычку, не обладающую индуктивностью, то конденсатор просто разрядился бы и на этом дело бы закончилось. Но катушка «сопротивляется» изменению тока в ней, благодаря явлению самоиндукции. За счёт этого ток в цепи растёт плавно, и конденсатор разряжается постепенно. При этом его энергия не теряется, а переходит в энергию магнитного поля катушки индуктивности.
И когда конденсатор полностью разрядился, ток в цепи продолжает поддерживать катушка индуктивности благодаря всё той же самоиндукции. Только на этот раз она препятствует не увеличению тока, а его уменьшению. В этом смысле катушка индуктивности похожа на тяжелую тележку, которую трудно разогнать, но затем также трудно затормозить, в виду сил инерции. Итак, катушка стремится поддерживать прежний ток, затрачивая на это энергию, накопленную в магнитном поле. Этот ток снова заряжает конденсатор, правда, уже в противоположной полярности. Когда энергия магнитного поля катушки полностью иссякнет, конденсатор окажется заряженным. И цикл повторится снова, только направление токов поменяется на противоположное.
Таким образом, в контуре возникают электромагнитные колебания: энергия постоянно перетекает туда-обратно между конденсатором и катушкой, ток в цепи меняется от максимального до нулевого и снова до максимального но с обратным знаком.
Собственная частота колебательного контура
Какова будет частота этих колебаний? Она зависит от параметров конденсатора и катушки индуктивности, и вычисляется по формуле Томсона:
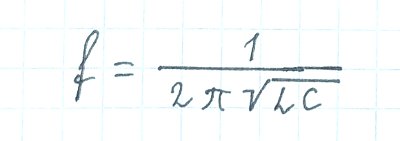
Формула Томпсона для расчёта частоты колебательного контура. L - индуктивность катушки (Гн), C - ёмкость конденсатора (Ф)
Чем больше ёмкость и индуктивность, тем медленнее конденсатор и катушка накапливают и отдают энергию, и тем ниже будет частота.
Также следует отметить, что на резонансной частоте реактивные сопротивления катушки и конденсатора равны. То есть частота собственных колебаний автоматически устанавливается такой, чтобы катушка и конденсатор получали одинаковые порции энергии.
Добротность
Но, конечно, такие колебания не могут длиться вечно. Как и в каждой реальной системе, здесь есть силы сопротивления. Поэтому на каждом цикле часть энергии тратится на преодоление этого сопротивления и уходит из системы в виде рассеивающегося тепла. Поэтому без внешней подпитки электромагнитные колебания будут затухающими:
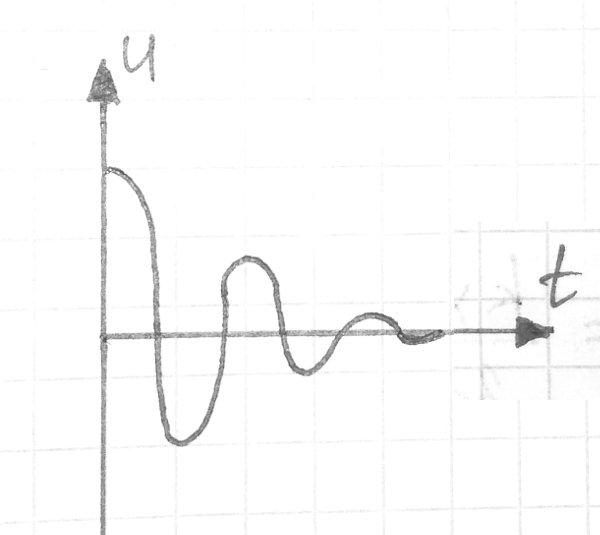
Затухание колебаний. Зависимость амплитуды (U, вольт) от времени t
Иногда, чтобы явно показать наличие сопротивления в колебательном контуре, в его схему добавляют «условный» резистор, который отражает все потери в проводах, конденсаторе и т.п.:
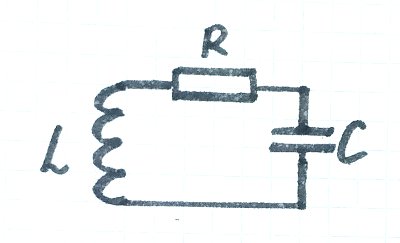
LCR-контур
Чтобы узнать, насколько много энергии теряется в колебательном контуре, вводят такую характеристику, как добротность. Собственно, это и есть соотношение запасаемой и теряемой на каждом цикле энергии. Чем выше добротность, тем дольше будут затухать колебания. А вот и формула добротности:
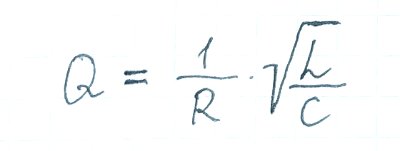
Формула добротности
Из формулы видно, что чем больше индуктивность L и чем меньше ёмкость C, тем выше добротность. Нетрудно понять, почему так происходит. Дело в том, что на каждом цикле вся энергия системы делится на две части. Одну часть безвозвратно поглощает активное сопротивление R, другая часть достаётся накопителю (конденсатору или катушке) или реактивному сопротивлению. Какая часть кому достанется, зависит от соотношения этих сопротивлений. Иными словами, добротность — это отношение реактивного и активного сопротивлений.
Напомню, что для катушки реактивное сопротивление пропорционально индуктивности L, а для конденсатора обратно пропорционально ёмкости C. Воспользовавшись тем, что на собственной частоте контура реактивные сопротивления катушки и конденсатора равны, как раз и можно вывести вышеприведённую формулу добротности.
Отсюда интересное следствие. Если стоит задача увеличить добротность, сохранив при этом частоту колебаний, следует увеличивать L и во столько же раз уменьшать C.
Механическая аналогия
Иногда сложно бывает понять процессы в электрических схемах, потому что все эти параметры: заряд, напряжение, ток, магнитное поле — всё же несколько абстрактны. Поэтому, мы воспользуемся аналогией с механической системой, которую легко представить и поведение которой «очевидно» из нашего жизненного опыта. А именно, рассмотрим пружинный маятник.
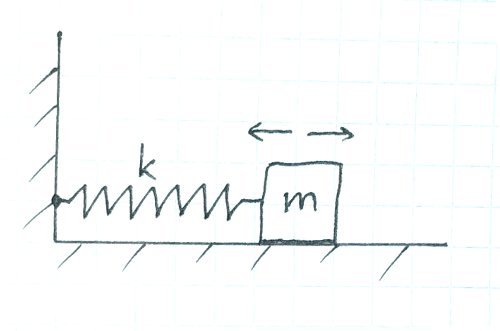
Пружинный маятник. k - коэффициент упругости пружины, m - масса грузика
Пружинный маятник представляет собой груз, закреплённый на пружине, второй конец которой жестко зафиксирован. Груз может скользить по гладкой поверхности. Если этой системе сообщить начальную энергию (например, сжав пружину), то она начнёт совершать свободные колебания относительно точки равновесия, также описываемые гармоническим законом.
Пружина — это аналог конденсатора. Конденсатор в цепи препятствует изменению напряжения. Если попытаться повысить напряжение, то конденсатор не даст изменить его резко, скачком. Начнётся сравнительно растянутый во времени процесс заряда конденсатора. И наоборот, если внешнее напряжение падает, конденсатор будет стремиться удержать его на прежнем уровне, отдавая часть своего заряда.
Пружина тоже сопротивляется изменению своей длины. Если мы будем её сжимать или растягивать, это всегда будет сопровождаться накоплением энергии в пружине или же наоборот, высвобождением энергии (в зависимости от того, движемся ли мы к положению равновесия или от него).
Ну а грузик — это аналог катушки индуктивности. Грузик сопротивляется изменению скорости аналогично тому, как катушка индуктивности препятствует изменению тока.
В колебательной системе всегда два накопителя энергии. В нашем маятнике это потенциальная энергия сжатой пружины и кинетическая энергия грузика. Обмен энергией между ними приводит к возникновению колебаний. Чтобы окончательно убедиться в аналогии между механическими и электромагнитными колебаниями, давайте сравним формулы частоты колебаний:
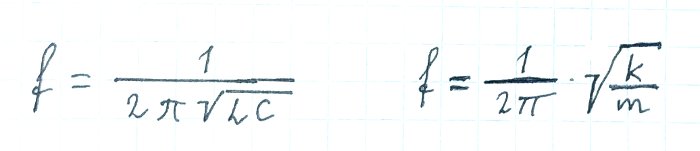
Cравнение формул частоты колебательного контура (слева) и пружинного маятника (справа)
Если принять, что 1/k — это аналог С, то, получается, формулы полностью идентичны. Остался только вопрос, почему 1/k — это аналог C. Дело в том, что чем больше ёмкость конденсатора, тем менее он «жесткий» - то есть меньше работы нужно произвести, чтобы загнать в него единицу заряда. Энергия, запасённая конденсатором, обратно пропорциональная емкости, а энергия пружины прямо пропорциональна её упругости, вот формулы:
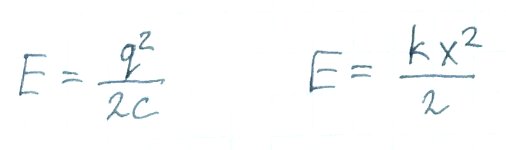
Формула энергии заряженного конденсатора (слева) и энергии сжатой пружины (справа)
Обращаю внимание, и в том и в другом случае частота не зависит от амплитуды. Не важно, насколько большим напряжением мы зарядили конденсатор или насколько сильно сжали пружину. От количества вложенной в систему энергии будет зависеть только «размах» колебаний, амплитуда, частота же останется постоянной.
Применение колебательного контура
Собственная частота колебательного контура одновременно является и резонансной частотой. На резонансной частоте общее сопротивление параллельного колебательного контура является максимальным. Поэтому его используют как элемент фильтров: когда из сложного сигнала с запутанным спектром нужно выделить узкий диапазон частот. Колебательный контур как раз и выделяет частоты, близкие к резонансной, заметно ослабляя более низкие (закорачивая их через низкое реактивное сопротивление катушки) или более высокие частоты (они уходят через низкое сопротивление конденсатора).
К примеру, колебательный контур часто располагают на входе радиоприёмника: он позволяет выделять из всего спектра радиочастот сигнал только одной радиостанции. Причём этот контур можно сделать перестраиваемым, заменив постоянный конденсатор на подстроечный, ёмкость которого можно менять поворотом ручки. Так что приёмник сможет настраиваться на разные радиостанции.
Также колебательный контур может быть элементом генератора, задавая его рабочую частоту. Нужно только сделать положительную обратную связь: усилить сигнал, полученный от контура, а затем часть этого усиленного сигнала вернуть обратно в контур, компенсируя таким образом все возможные потери и делая колебания незатухающими.




Добавить комментарий